Thursday, October 29, 2015
My new main squeeze (mathematically speaking) - Desmos Activity Builder
Over the last couple of months, I have become more and more familiar with the brilliance of Desmos Activity Builder (found at the bottom left of this linked page). My students have become quite familiar with activity builder as well. For the last number of years, I have been deeply appreciative of the good product put out by Desmos. The online calculator is intuitive and really helps students to grasp the conceptual in a way that allows mathematical procedures to have a firm grounding (supporting the effective mathematics teaching practice 6 as defined within NCTM's Principles to Actions). The relatively new feature of the activity builder has taken it to an entirely different level.
While I have used it in my college classes to support the understanding of my students, it has also been enjoyable to see my methods students develop their own activity builder lessons. My great successes within activity builder have centered around student discovery of transformations of functions. Yesterday, my college algebra students engaged in this activity.
https://teacher.desmos.com/activitybuilder/custom/562e3e7f9236025b1c09a483
I had students work in groups, primarily pairs on this activity. I did this to allow my students to have discussions about their mathematical assertions. Using collaborative groupings allows for students to have meaningful mathematical discourse as defined in effective mathematics teaching practice 4 within Principles to Actions.
As students are engaged in the activity, I can monitor progress through the overview page on the teacher dashboard of activity builder. I really appreciate this feature because I am able to monitor the ways that students are progressing through the activity. I don't want speed to be a factor in my instruction, so if a group seems to be rushing through the activity, I know this right away. I can check in with this group to monitor more closely their needed understanding of the concepts.
Another of the wonderful aspects of activity builder is that I can check student work easily after the students have completed the activity in class. At the end of this particular activity, I asked my students to find three different quadratic functions that would match to the curves on my "ugly mug" picture. This was the creation of one group.
Desmos is also a fertile ground for students to work on appropriate vocabulary within particular contexts. As I monitor their responses, I can step in and ask probing questions to add a certain level of mathematical specificity to their written assertions in Desmos.
In short, activity builder has allowed me to create an environment where the sense making is placed firmly on the shoulders of my students. They are actively engaged in the content as they explore the behavior of functions. It is a great environment for students to take risks and revise thinking.
Thank you, Desmos!
Monday, September 21, 2015
Emazing presentations
At our most recent School of Education retreat at the beginning of this academic year, my dean (Dr. Michael Uden) introduced us all to a presentation tool by the name of Emaze. In some ways, it reminded me of Prezi. However, it had a little more staying power in terms of visual appeal (for me at least). I decided to take action on Dr. Uden's inspiration to transform one of my old Prezi's for my Number Sense course and turn it into an Emaze experience.
The reality with any presentation tool is that it can easily just be a fancy-dancy PowerPoint presentation. This ought not to be the goal. Active student engagement needs to be at the center of any presentation. I will be using the Emaze presentation found below in my class tomorrow. I plan to take significant amounts of time to pause and have the students engage each other at their tables in discussion centered around deductive reasoning and problem solving.
At the very least, Emaze is another tool for implementing the potential for an engaging learning environment. We shall see what tomorrow holds!
Click to see Dr. Paape Math 119 Section 2.3 Emaze Presentation
The reality with any presentation tool is that it can easily just be a fancy-dancy PowerPoint presentation. This ought not to be the goal. Active student engagement needs to be at the center of any presentation. I will be using the Emaze presentation found below in my class tomorrow. I plan to take significant amounts of time to pause and have the students engage each other at their tables in discussion centered around deductive reasoning and problem solving.
At the very least, Emaze is another tool for implementing the potential for an engaging learning environment. We shall see what tomorrow holds!
Click to see Dr. Paape Math 119 Section 2.3 Emaze Presentation
Tuesday, September 15, 2015
Rubric to support the expression of student reasoning
Before the beginning of this school year, I spent quite a bit of time reflecting on my teaching practice as a whole. In many ways, my regular day-to-day practice has radically changed to fall much more in line with what we know to be best practices in math education based on research. However, my assessment strategies have lagged pretty far beyond. Today, in my Number Sense course I am trying something new. I am curious to find out if my adjustment increases the quality of the ways my students express their reasoning, or if I have removed some of the cognitive load for them. Here's what I did.
1. I made most of the assessment very pattern-oriented. For instance, I included a number of problems like the ones below.
I found the patterns above at www.visualpatterns.org/
2. At the beginning of the quiz, I previewed the problems with the class. I also showed them a problem solving rubric that I would be using to assess their explanations of their reasoning within their problems. I kept this rubric visible on the front screen throughout the quiz.
I adapted this rubric from a Utah Education Network website. I intentionally changed the rubric slightly to embed some Growth Mindset vocabulary in the "Not Yet" column of the rubric.
3. As students worked on the quiz, I observed them regularly looking up at the rubric. As I consider the value of this rubric, my one concern is that I may have removed a small amount of the cognitive load for my students. However, I think the rubric is general enough that it will likely serve more as a guide than a crutch for the students.
Here are a couple of samples of student work done within the rubric framework.
I'm pretty happy with the detailed nature of the work of my students. As is often the case with pattern problems, it is interesting to see the variety of ways that students see the math within the problem.
I plan to continue to inspect my assessment strategies for more ways to facilitate deeper student thinking.
1. I made most of the assessment very pattern-oriented. For instance, I included a number of problems like the ones below.
I found the patterns above at www.visualpatterns.org/
I adapted this rubric from a Utah Education Network website. I intentionally changed the rubric slightly to embed some Growth Mindset vocabulary in the "Not Yet" column of the rubric.
3. As students worked on the quiz, I observed them regularly looking up at the rubric. As I consider the value of this rubric, my one concern is that I may have removed a small amount of the cognitive load for my students. However, I think the rubric is general enough that it will likely serve more as a guide than a crutch for the students.
Here are a couple of samples of student work done within the rubric framework.
I'm pretty happy with the detailed nature of the work of my students. As is often the case with pattern problems, it is interesting to see the variety of ways that students see the math within the problem.
I plan to continue to inspect my assessment strategies for more ways to facilitate deeper student thinking.
Monday, September 7, 2015
The Department of Representations Department
The use and connection of mathematical representations is one of the eight effective mathematics teaching practices put forward by the National Council of Teachers of Mathematics (NCTM) within their 2014 publication, Principles to actions: Ensuring mathematical success for all. The idea of representing concepts within mathematics is nothing new for those of us in math education. However, I think that the use of representations and emphasis of using representations in an interchangeable manner serves to further promote the understanding of concepts for students. In this post, I am going to reflect on a Week 1 activity that I drastically changed from my old practice of teacher-centered instruction to one where student representations and discourse took center stage.
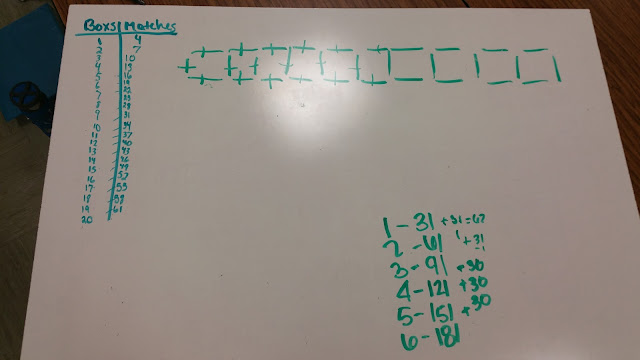
This was the only solution of its kind. This group actually struggled quite a bit to get to a solution. They had initially misread the problem and had added matchsticks below the original figure, not as a continued horizontal pattern. However, when they regrouped, reanalyzed the problem, a new solution strategy emerged. This group noticed that they could represent the first ten matchstick boxes as drawn on their board. They then thought that they could do six more of these groups of 10. Initially, this was met with a problem. "We have too many sticks." Another adjustment was made to remove the 1 overlapping matchstick. Therefore, they knew to not continually add the 31 sticks from the first 10 boxes, but rather 30 sticks to account for the overlapping stick. WONDERFUL!
In recent months, there has been a bit of a commotion on Twitter in respect to Vertical, Non-permanent Spaces. Take a look at Alex Overwijk's blog on the topic of VNPS. I have also blogged on my use of large table whiteboards as well in the past. VNPS have taken a prominent role in my teaching practice. What follows is an example of their use within an activity designed to allow for students to compare representation usage.
Here was the question for the class to consider.
This is a fun, little problem that allows for multiple points of interpretation by students. I asked the additional estimation/guess question to instill in students the idea that we want to have idea of where we are going with a problem before we begin.
Before I get into what the students did, I want to reflect a bit on how I have taught this in the past. In years past, I would stand at the board, marker in hand, and draw the picture (maybe putting a number 1, 2, 3, and 4 in each of the squares above. I would then write what is written below.
I would literally say exactly what it was that I wanted my students to notice. That is worth saying again - I would tell my students what THEY should notice. As I reflect on that teaching practice, I actually get pretty ashamed of that kind of teaching in my past. In my practice, I was stealing the learning moments from my students - taking away the opportunity for them to have ownership in the learning. Ultimately, after I had "led the witness" to the point that he or she may or may not have grasped what I had hoped to be learned, I would assume that he or she could then translate this decoding skill to other representations. For some, this was accomplished, but for the learner who struggled, this was rarely the case.
Fast forward to a Principles to actions classroom and a new mindset on my part. At the very forefront of my thinking, both in the preparation of my lessons and the implementation of those lessons, is the goal for my students to do the noticing. I want them to wonder about a problem, to discuss ideas with their collaborators at the table with them and for them to have ownership of their learning. Here are a series of representations created by my students after they were given a substantial amount of time to converse around the topic. Four somewhat different approaches surfaced from the various groups.
Creating a table to help
As you can see from these two groups, they noticed the same pattern of +3 that I had regularly shown my students in the past. The group in the top picture used a drawing to show where the 3 and the 1 in their pattern were. The group on the bottom (a group of math majors, unlike the top picture), used a series of growing matchstick representations. The complexity of the algebraic expression in their generalization was somewhat sophisticated. I didn't want to discount the value of their expression, but simply asked if they realized that this expression of 4+3(n-1) would be a sticking point for some younger learners. What does the n-1 stage mean? How can you relate your algebraic representation to your drawing? These students were able to explain their thinking but were open to the idea that this expression could cause confusion. All of these interactions would never had happened, if I was at the board telling them what to notice.
60 squares of 3, plus 1 extra stick
Each of the three groups above used some version of the fact that they needed 60 total squares. They identified that all of the squares with the exception of the very first square (with 4 matchsticks) were created by adding on three matchsticks.
56 more squares
Each of the groups above used an adding-on approach. Since they were given four original squares, they made the adjustment of adding on 56 additional squares with 3 matchsticks in each square.
We need 60 squares - here is what 10 is - we need 6 of those, plus adjustment
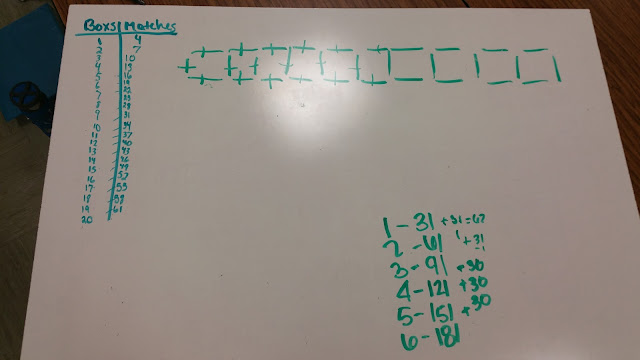
This was the only solution of its kind. This group actually struggled quite a bit to get to a solution. They had initially misread the problem and had added matchsticks below the original figure, not as a continued horizontal pattern. However, when they regrouped, reanalyzed the problem, a new solution strategy emerged. This group noticed that they could represent the first ten matchstick boxes as drawn on their board. They then thought that they could do six more of these groups of 10. Initially, this was met with a problem. "We have too many sticks." Another adjustment was made to remove the 1 overlapping matchstick. Therefore, they knew to not continually add the 31 sticks from the first 10 boxes, but rather 30 sticks to account for the overlapping stick. WONDERFUL!
Concluding thoughts
After each group finished their work on the whiteboards at their tables, I asked them to put their boards in the marker trays around the room. We all took a gallery walk to make sense of the work of our classmates and to ask clarifying questions, if needed. I encouraged the students to look for similarities and differences in methods used. Next, each group got to verbalize to the class the work they had done and processes used in getting solutions.
Taking this kind of time to get to an answer that I could have showed a class in much, much, much less time is an intriguing struggle. However, I am absolutely confident that my students have grown in varying degrees in their problem solving skills as a result of the intentional kind of struggle in creating their own representations of the math. Thanks again to the Department of Representations Department. It may seem redundant, but I do know that the students appreciate the idea of sharing thoughts with each other. They also appreciate seeing the varying ways that their classmates think about math. The ways in which I validate their efforts in an activity like this go a long way in furthering the growth mindset for each of the students in my classroom. It is a wonderful adventure we are on together to grow in our mathematical understandings.
Thursday, September 3, 2015
Group Dynamics 101
Today marks day four of a new school year. It has been a blast to put into use all of the new ideas I've been considering throughout the summer. One of the new implementations that has reaped immediate benefits is the use of the document below.
On the first day of my class, I had each student fill out this form. Not only did this give me a feel for the math dispositions of my students, but I was able to use this data to form some intentional heterogeneous groupings to best promote student discourse. I have always been a proponent for heterogeneous groupings, but never before I have been able to make these grouping choices based on student-identified markers. I have been very pleased thus far by the kind of work my groups have been doing. In addition to my intentional grouping strategy, I have had the students create a list of what they do and don't like about group work.
I really like the lists that my students created. I handed out this completed copy of group work norms to the students. We have all agreed that this is the standard to which we will hold ourselves in our group work. In my next post, I will blog on an activity that reaped the reward of my data-driven groupings and class-originated norms for group work.
Tuesday, September 1, 2015
New Beginnings
Yesterday marked the beginning of my 16th year of teaching. At the beginning of each year there is anxiety, hope, fear, joy, and anticipation. All of those emotions are shared by teacher and student alike. My first interactions with the 130+ students (many of which were college freshmen) I will have this semester have all been encouraging as I set out to influence each of these students to be better mathematicians and (for the majority) future educators.
As I consider my personal and professional intentions for this semester, I feel a deeper passion for meeting these goals than ever before. I can't exactly put my finger on why I am feel this increased passion, but it is there for a reason (whatever it may be). In simple terms, here are my goals for my classroom practice.
1. Increase student-to-student discourse to the point that it is the predominant form of communication in the classroom.
2. Make use of intentionally designed heterogeneous groupings to further promote discourse and productive struggle.
3. Make the work of students (in many and various forms) visible to the class so that work is collectively analyzed.
4. Promote a growth mindset.
5. Provide qualitative feedback to student work on assessments of all kinds.
6. Smile and show students that teaching is an amazingly rewarding profession.
Tuesday, June 9, 2015
Talking math with your kids #tmwyk
One of the wonderful privileges of being a parent is that we get to train our children in so many ways. One of my ways to nuture my children is through talking to them about mathematics. Sadly, for many who have had bad experiences with mathematics, this idea of talking math with children can cause anxiety. This does not have to be the case when we see math as the flexible, usable, adaptable, enjoyable beauty that it is.
On Twitter there is a hashtag, #tmwyk or talking math with your kids. This hashtag was created by Christopher Danielson. Christopher is very active on Twitter and quite responsive to individuals who post with the #tmwyk hashtag. You can check out Christopher's website here.
Over the last year or so, I have posted a number of interactions with my oldest daughter to the #tmwyk hashtag.
Using the Chromecast to #tmwyk pic.twitter.com/9yGWvLc9hu
— Adam Paape (@Adapaa) March 21, 2015
My kiddo and I were playing, "Which one doesn't belong?" in this tweet. Christopher Danielson is responsible for the "Which one doesn't belong?" game.
Fun work with multiples of three based on this glass of milk. 5 year old loves it. #tmwyk pic.twitter.com/FszNjPMtZP
— Adam Paape (@Adapaa) November 2, 2014
Here we had a wonderful conversation about multiples that she started by noticing the threes.
This morning my daughter and I spent some time playing a card game. I found this card game here. The basic idea is that you lay down 7 cards and then the kiddo tries to find two cards that add up to 10.
The child continues to find pairs of 10s until there are no more pairs. When there are no more pairs to be made, the parent puts down seven more cards and the child tries to find pairs of 10s again.
In our first attempt at this game, my daughter was clearly excited. We had a really nice conversation about an Ace (1) plus 9. We discussed whether or not 1+9 was the same as 9 + 1. Talk about a great way to think about the commutative property of addition. My daughter said, "Yes Daddy, they are the same." I said, "Why are they the same?" At first she said, "Well, just because they are." But then she gave me a counterexample. "Dad, it isn't 9+2." I said, "That's really good kiddo. Thank you for your thought and thank you for making me think."
After a little while we put down 7 more cards. An interesting thing happened with this sequence. Take a look.
I asked her, "What do you notice." I was expecting that she would identify the patterns of the Aces and the 9s. However, she had a very different thought in mind. She told me, "Well Dad, these two are the only two that are black." I said, "Wow! You noticed something I didn't even see." She looked at me with a huge smile. She was so proud to have noticed something that Dad didn't see.
I love activities like this where there are many possibilities for different perspectives on the math. On this particular sequence of seven cards, I thought that she would just pick up all the Aces + 9 to get her 10s, but she didn't do that. She remembered that there was another 5 that was hidden under one of the 9s, so she worked to get an Ace plus 9 so that she could get to a 5 + 5 because, as she said, "I know 5 + 5 is 10." Wonderful, this is why we talk math with ours kids. They will show us things that we didn't even think about. Kids will create strategies that are all their own and it is one of our jobs to get them to justify their reasoning behind these wonderful, kid-created strategies and thoughts. So, let's keep the #tmwyk movement going - the payoff is huge!
Monday, June 8, 2015
Growth mindset in the classroom
">
A number of weeks back I had the pleasure of listening to Jo Boaler speak at the Wisconsin Mathematics Council annual conference. She spoke to us about many aspects of best practices in mathematics education. One of her main points was that we need to make a transition within our students from a fixed mindset to a growth mindset. Boaler referenced Carol Dweck's research on mindset. Dweck makes the point that students need to realize that their brains literally grow when they are challenged in the classroom. When a child is given a complex problem, the teacher needs to encourage the students that they can do this and that this challenge will grow their brains- the challenge is good. Dweck highlights the idea of "not yet" as an important way for teachers to think about assessment of students. She mentions that students who have a growth mindset really do see learning as a valuable endeavor.
See Dweck's Ted Talk on "The Power of Yet" below.
See Dweck's Ted Talk on "The Power of Yet" below.
As I think about this growth mindset and the idea of not labeling students as smart or dumb, I feel like this is something we ought to be doing already. However, it really isn't the case. And, I'm sure that I am guilty of unknowingly labeling my students in the various ways that I treat them. Many students see themselves as smart or as dumb (fixed mindset). Teachers need to be intentional in articulating to students that the lessons teacher's design are meant to be challenging and that hard work does pay off through perseverance and persistence. Within the Common Core Standards for Mathematical Practice, there is a standard (SMP1) that highlights the benefits of perseverance in problem solving. Any teacher of mathematics ought to realize that persistence in problem solving is a valuable trait, but often times we really struggle to get this trait to be manifest within our students. Therefore, this intentional focus on perseverance is something that a teacher needs to purposefully cultivate in his or her classroom practice.
I have spent quite a bit of time with my 6-year old, helping her to see the value of hard work both in her reading and in her work with mathematics. The other night we were working on her leveled readers and she was working hard and struggling, but I told her, "Sweetie, you can do this. It is hard work, but hard work pays off. Let's keep trying." Eventually, after working really, really hard on a lot of words, she said, "Dad, I can do this! I can read!" She was so proud of her hard work. She experienced "not yet."
The other day we received a document from her school of a self-analysis that she did within a book called, "If I lived in a castle." You can see the image below. She identified herself as "Lady [her name] the Smart." I'm not too concerned about this, but I do find it interesting that she is already labeling herself "the smart."
So, take another look at Carol Dweck's video and think about the idea of a fixed mindset versus a growth mindset. As an educator, my goal for my students and my children is that they have growth mindsets. It is work, but it is worthwhile work that pays huge dividends in learning and brain development.
I have spent quite a bit of time with my 6-year old, helping her to see the value of hard work both in her reading and in her work with mathematics. The other night we were working on her leveled readers and she was working hard and struggling, but I told her, "Sweetie, you can do this. It is hard work, but hard work pays off. Let's keep trying." Eventually, after working really, really hard on a lot of words, she said, "Dad, I can do this! I can read!" She was so proud of her hard work. She experienced "not yet."
The other day we received a document from her school of a self-analysis that she did within a book called, "If I lived in a castle." You can see the image below. She identified herself as "Lady [her name] the Smart." I'm not too concerned about this, but I do find it interesting that she is already labeling herself "the smart."
So, take another look at Carol Dweck's video and think about the idea of a fixed mindset versus a growth mindset. As an educator, my goal for my students and my children is that they have growth mindsets. It is work, but it is worthwhile work that pays huge dividends in learning and brain development.
Monday, May 18, 2015
My biggest success of the 2014-2015 school year. Big board math.
"Teacher, can I please be board?"
Yes, I did spell "board" correctly. At the end of this semester's final exam for my Math119 Number Sense course I provided my students with an opportunity to give me some feedback on a variety of strategies/technologies I had implemented. One of these was the use of three foot by two foot whiteboards for table work. In short, this was a HUGE success.
I have always been a proponent of getting students to look at the work of others. However, the ways in which we accomplish this can be varied, both in structure and effectiveness. In the past, I have had groups work together in ways to communicate a concept or to solve a problem that would only allow the kids to put their work under the document camera or to transcribe all of their work at the board. Both of these methods were inefficient and had drawbacks in terms of the ability for the entire class to stay engaged in the process. My math classroom at Concordia has always had small, individual whiteboards for class use. While these whiteboards were decent for individual work, they didn't work very well at all for collaborative work. In steps the big whiteboard.
Our local Home Depot sells 32 ft square paneling that works great for whiteboards. Not only is this paneling inexpensive ($13.97 a sheet), but the wonderful people at Home Depot will cut it to size for you. Including tax, I was able to spend less than $30 to equip my room with eight three-foot by two- foot boards and four two-foot by two-foot boards.
On one particular day of the semester, I was introducing ideas of operations with fractions. All of these pre-service teachers had some level of prior knowledge with the concepts covered. I decided to use the big boards to let them show me (and each other) what they knew. I intentionally wanted to see if they could recall/describe more than just a blind procedure in respect to the operations.
Here is what the students were prompted to do.
Table Task
1. How
would you describe your given fraction operation to a student?
2. Where
do you think they might get confused?
3. Can
you think of a way to help them deal with the confusion? How?
4. Is
there a way to represent your operation with a model/drawing?
As you can see from the big boards, some were able to make some solid group representations, some were not able to do so.
One of the many wonderful aspects of big board work is that the boards can easily remain visible for the duration of class time. I noticed students referring to the work of classmates throughout our conversations that day. My six foot square boards rested nicely within the marker trays. As you can see, I took pictures of the boards for later use. I noticed students doing this as well. I can easily see the use of Padlet.com for easy reference at a later time for students.
By nature, big board work at tables forces the members of a group to lean in to the table to work together on the board. As I have implemented more big board work, I have heard some wonderful mathematical arguments about what one group member saw as relevant for the group's representation.
This sort of collaboration and cooperation is to be firmly entrenched with the best practices mathematics classroom. SMP 3 is a bedrock of this sort of activity, as students are encouraged to diagnose the big board work of others. Students are prompted to ask questions of other students, not the teacher. In the somewhat new document put out by the National Council of Teachers of Mathematics (NCTM) entitled, "Principles to Actions: Ensuring Mathematical Success for All," a clarion call for mathematics instruction is established for our schools. In this book, the NCTM writers lay out eight focal points that describe good math teaching. Two of these focal points are naturally a part of big board work - facilitate meaningful mathematical discourse and elicit and use evidence of student thinking. In short, big board work (regardless of the content) is fertile ground for the kind of teaching we all should be doing within the math classroom.
I have also made use of the big boards to facilitate discussions on homework at the beginning of class. As students enter the room, I assign each table one problem from the homework from the previous night. Sometimes more than one group will work together on a problem from the night before. While the group is determining how best to represent their answer, I am floating throughout the room checking for completion of individual work from the night before. When a table is done working out their response on their board, they put it up in a marker tray. In about five minutes, the room has become a discourse magnet, both at tables and throughout the greater room. After this brief and efficient amount of time, we can move on to our inquiry/discovery/discussion of the day.
For the twenty-one students who responded to my request for feedback on my teaching strategies throughout the semester, they gave the big boards an average score of 9.2 on a ten point scale. The next closest strategy/technology was Plickers (I will blog on this at a later time). It is safe to say that my students enjoyed working together, getting up out of their seats, standing, and talking about the beautiful math. Good stuff!
These were my initial successes with big board math. Do you have any ideas on how I could make this even better? I welcome all thoughts.
Tuesday, May 12, 2015
A funny thing happened on the way to the chalkboard.
1. Students enter the room with last night's homework.
2. The first fifteen minutes (or more) are spent on going over the homework problems. These problems of discussion are typically selected by the highest achievers in class, leaving those with deeper misconceptions left to sit back and watch (or not watch).
3. The next 20 to 30 minutes is the teacher explaining a procedure or concept to the best of his or her ability.This often includes the teacher writing his or her notes/examples on the board. The students are then putting down in their notes exactly what is written of the board. When the highest achievers have questions about a process or product, the teacher will do another example similar to the first, but with different numbers.
4. Fifteen to 20 minutes are dedicated to doing homework in class that is an additional set of problems just like the examples during the lesson. When problems diverge in thinking from the examples, these are seen as the really, really hard problems.
Truth be told, this was my teaching style of mathematics for many years. In fact, the first few iterations of my Number Sense class were much like this. Any teacher who has taught in this traditional format can relate to the frustration that, "My students got it yesterday when I taught them, but today it is like they have never seen it before." Sound familiar? It does to me.
Over the years, I have used an article in my methods and curriculum class for future teachers of middle school and high school students. This article is written by Stephen Reinhart and was originally published by the National Council of Teachers of Mathematics. The article can be found here. In "Never say Anything a kid can say," Reinhart proposes a student-centered classroom where the power of collaboration is king. While Reinhart wrote this article over a decade ago, the themes and strategies highlighted are still very true in math education. In fact, the Standards for Mathematical Practices (SMP) within the Common Core State Standards for Mathematics CCSSM), emphasize the very same conversational environment within SMP3. SMP 3 can be found here. In SMP 3, students are required to construct viable arguments and to critique the reasoning of others.
This requirement of argument and critique begs a certain question in respect to traditional mathematics instruction. Is it possible (or at least likely) that students are regularly given the opportunity to construct mathematical arguments that are viable? Do they critique the reasoning set forth by their classmates? I would respond to those questions with an emphatic, "NO!"
This brings me back full circle to my Number Sense class. I used to a "good job" telling my students exactly what I knew about improper fractions and division with decimal squares, but I never gave them the opportunity to discover, inquire, and converse about what they knew. This has changed completely in my most recent versions of the course. I always have in mind, "Don't tell them, have them do something to create a group understanding at their tables."
I plan to blog in much more depth about my use of technologies (Nearpod, Plickers, Padlet, Aurasma, Kahoot, Desmos, and others) and other engagement strategies (Big Whiteboards [2 feet by 3 feet boards for tablework], speed dating, and "Let the chalk (not really chalk) do the talk").
So, a funny thing did happen on the way to the chalkboard, because now I am no longer on my way to the chalkboard to be a grand orator of math knowledge. I want to create an environment where the voice of the student is the predominant voice heard in my room. Research shows that with the right coaching, kids can thrive in this kind of environment and actually see math as much, much more than notes, blind procedures, and something that they are just not good at.
Saturday, May 9, 2015
My blogging life begins
This past week from May 6th to May 8th I had the pleasure of attending the Wisconsin Mathematics Council's (WMC) annual conference in Green Lake, WI. While this three-day period of math teacher bliss was wonderful, it was a significant amount of time away from my beautiful family. I appreciate their sacrifice to allow me to re-energize and re-think my teaching practice.
I had the pleasure of sitting in on a number of very good sessions. One session, in particular, was a session on how to be a life-long learner in your pajamas! Great idea! Well, the presenter inspired me to think about starting my own blog. Here it is.
I plan to write about my teaching practice as a university professor in mathematics education. I am already a pretty reflective teacher. However, I rarely compose my thoughts in a narrative form. I will also think out loud in respect to my new role as a board member for the WMC. I am honored to have been elected to this position. I consider it a great responsibility to help shape the vision for mathematics instruction in our wonderful state. One of the vision points for this upcoming year (as highlighted by the current WMC president) is to start a university student affiliate group. OUTSTANDING! I was already blessed to bring eighteen of my math education pre-service teachers with me this year to WMC. Dare I dream to bring fifty next year? I would be proud to have my Concordia University Wisconsin students seen as the exemplar for active, involved future educators in mathematics.
Well, there it is - my first blog.
Hopefully, there is more to come within my renewed curiosity.
Subscribe to:
Comments (Atom)








































