In recent months, there has been a bit of a commotion on Twitter in respect to Vertical, Non-permanent Spaces. Take a look at Alex Overwijk's blog on the topic of VNPS. I have also blogged on my use of large table whiteboards as well in the past. VNPS have taken a prominent role in my teaching practice. What follows is an example of their use within an activity designed to allow for students to compare representation usage.
Here was the question for the class to consider.
This is a fun, little problem that allows for multiple points of interpretation by students. I asked the additional estimation/guess question to instill in students the idea that we want to have idea of where we are going with a problem before we begin.
Before I get into what the students did, I want to reflect a bit on how I have taught this in the past. In years past, I would stand at the board, marker in hand, and draw the picture (maybe putting a number 1, 2, 3, and 4 in each of the squares above. I would then write what is written below.
I would literally say exactly what it was that I wanted my students to notice. That is worth saying again - I would tell my students what THEY should notice. As I reflect on that teaching practice, I actually get pretty ashamed of that kind of teaching in my past. In my practice, I was stealing the learning moments from my students - taking away the opportunity for them to have ownership in the learning. Ultimately, after I had "led the witness" to the point that he or she may or may not have grasped what I had hoped to be learned, I would assume that he or she could then translate this decoding skill to other representations. For some, this was accomplished, but for the learner who struggled, this was rarely the case.
Fast forward to a Principles to actions classroom and a new mindset on my part. At the very forefront of my thinking, both in the preparation of my lessons and the implementation of those lessons, is the goal for my students to do the noticing. I want them to wonder about a problem, to discuss ideas with their collaborators at the table with them and for them to have ownership of their learning. Here are a series of representations created by my students after they were given a substantial amount of time to converse around the topic. Four somewhat different approaches surfaced from the various groups.
Creating a table to help
As you can see from these two groups, they noticed the same pattern of +3 that I had regularly shown my students in the past. The group in the top picture used a drawing to show where the 3 and the 1 in their pattern were. The group on the bottom (a group of math majors, unlike the top picture), used a series of growing matchstick representations. The complexity of the algebraic expression in their generalization was somewhat sophisticated. I didn't want to discount the value of their expression, but simply asked if they realized that this expression of 4+3(n-1) would be a sticking point for some younger learners. What does the n-1 stage mean? How can you relate your algebraic representation to your drawing? These students were able to explain their thinking but were open to the idea that this expression could cause confusion. All of these interactions would never had happened, if I was at the board telling them what to notice.
60 squares of 3, plus 1 extra stick
Each of the three groups above used some version of the fact that they needed 60 total squares. They identified that all of the squares with the exception of the very first square (with 4 matchsticks) were created by adding on three matchsticks.
56 more squares
Each of the groups above used an adding-on approach. Since they were given four original squares, they made the adjustment of adding on 56 additional squares with 3 matchsticks in each square.
We need 60 squares - here is what 10 is - we need 6 of those, plus adjustment
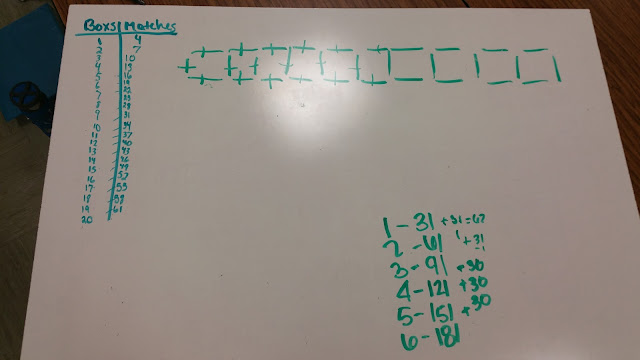
This was the only solution of its kind. This group actually struggled quite a bit to get to a solution. They had initially misread the problem and had added matchsticks below the original figure, not as a continued horizontal pattern. However, when they regrouped, reanalyzed the problem, a new solution strategy emerged. This group noticed that they could represent the first ten matchstick boxes as drawn on their board. They then thought that they could do six more of these groups of 10. Initially, this was met with a problem. "We have too many sticks." Another adjustment was made to remove the 1 overlapping matchstick. Therefore, they knew to not continually add the 31 sticks from the first 10 boxes, but rather 30 sticks to account for the overlapping stick. WONDERFUL!
Concluding thoughts
After each group finished their work on the whiteboards at their tables, I asked them to put their boards in the marker trays around the room. We all took a gallery walk to make sense of the work of our classmates and to ask clarifying questions, if needed. I encouraged the students to look for similarities and differences in methods used. Next, each group got to verbalize to the class the work they had done and processes used in getting solutions.
Taking this kind of time to get to an answer that I could have showed a class in much, much, much less time is an intriguing struggle. However, I am absolutely confident that my students have grown in varying degrees in their problem solving skills as a result of the intentional kind of struggle in creating their own representations of the math. Thanks again to the Department of Representations Department. It may seem redundant, but I do know that the students appreciate the idea of sharing thoughts with each other. They also appreciate seeing the varying ways that their classmates think about math. The ways in which I validate their efforts in an activity like this go a long way in furthering the growth mindset for each of the students in my classroom. It is a wonderful adventure we are on together to grow in our mathematical understandings.










No comments:
Post a Comment